The Pythagorean Triple is a relation among the three sides of a right triangle.
The theorem is as follows:
The sum of the areas of the two squares on the legs (a and b) equals the area of the square on the hypotenuse (c).
If we let c be the length of the hypotenuse and a and b be the lengths of the other two sides, the theorem can be expressed as the equation:
I used 6 as my a and I used 8 as my b.a² + b² = c²
36 + 64 = 100
6² + 8² = 10²
Click here to see how to find the missing leg of a right triangle.
Click here to see how to find the missing hypotenuse of a right triangle.
You're locked out of your house and the only open window is on the second floor, 25 feet above the ground. You need to borrow a ladder from one of your neighbors. There's a bush along the edge of the house, so you'll have to place the ladder 10 feet from the house. What length of ladder do you need to reach the window?
My own word problem.
Two joggers run 8 miles north and then 5 miles west. They discovered that there is another way to go back to their starting point. They went from west straight to north without turning. How many miles did they travel from west back to north?
36 + 64 = 100
6² + 8² = 10²
Click here to see how to find the missing leg of a right triangle.
Click here to see how to find the missing hypotenuse of a right triangle.
You're locked out of your house and the only open window is on the second floor, 25 feet above the ground. You need to borrow a ladder from one of your neighbors. There's a bush along the edge of the house, so you'll have to place the ladder 10 feet from the house. What length of ladder do you need to reach the window?
My own word problem.
Two joggers run 8 miles north and then 5 miles west. They discovered that there is another way to go back to their starting point. They went from west straight to north without turning. How many miles did they travel from west back to north?
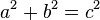
No comments:
Post a Comment