Jann's 2nd Scibe

Sorry this scribe is late, i forgot to finish it during the weekends.
Well, this scribe is about the Pythegorean Triple.

First, What is the Pythergorean Triple?

The Pythegorean Triple is a right angle triangle that uses a set of numbers such as 1,2,3,etc. This set of numbers has to be a decimal, also this set of numbers has to satisfy a² + b² = c²

For example, this set of numbers can be 3,4,5. Since 3² is equal to 9, 4² is equal to 16 and 5² is equal to 25. a² = 3 , b² = 4 , c² = 5²

If you put that in a diagram it would look like this...

You notice that C² is always the hypotinus. The hypotinus is the the line conecting 3² and 4² together, The vertical line and the horizontal line can be a² or b² usually, the vertical line is a² and the horizontal is b².

Kevin Y's Pythagoras Growing Post

Part 1 : Pythagorean Triple

A Pythagorean Triple is a right triangle that uses a set of whole numbers (1, 2, 3, etc..) used to satisfy the problem a² + b² = c².



The example im going to use is 3² + 4² = 5². There are other triples as well, like 6² + 8² = 10².

Part 2 :

Part 3 :

You're locked out of your house and the only open window is on the second floor, 25 feet above the ground. You need to borrow a ladder from one of your neighbors. There's a bush along the edge of the house, so you'll have to place the ladder 10 feet from the house. What length of ladder do you need to reach the window?

Part 4 :

If you needed to throw a waterballon up onto rooftop thats 10 meters tall, and you were 15 meters away how high and how far would you have to throw the waterballoon?

Angelo's Pythagoras Growing Post

Part1:
A Pythagorean Theorem is when the legs of a right triangle ( a & b ) and the hypotenuse obey the following relationship " a2 + b2 = C2."

A Pythagorean Triple is a right triangle that uses a set of numbers (1,2,3,etc...) that satisfy a2 + b2 = C2. The set of numbers can't have any decimals For example, 3squared + 4squared = 5squared.Another way to say that is, 9 + 16 = 25.

I had to figure out another Pythagorean Triple using only the Perfect Squares up to ten. The perfect squares are:
1 x 1 = 1
2 x 2 = 4
3 x 3 = 9
4 x 4 = 16
5 x 5 = 25
6 x 6 = 36
7 x 7 = 49
8 x 8 = 64
9 x 9 = 81
10 x 10 = 100
The next Pythagorean Theorem after 3 squared + 4 squared = 5 squared is, 6 squared + 8 squared = 10 squared. I proved it in three different visual ways.
The first one I used the right triangle. It is clear that the legs will add up to the hypotenuse.

The second way, i proved it in squares. It is clear that 36 squares (6 squared) + 64 squares (8 squared) will equal 100 squares (10 squared).

The third way, I showed it in squares again. You could see that the a2 and b2 fits in c2 perfectly.


Part 2:
BubbleShare: Share photos - Powered by BubbleShare

For the missing hypotenuse, I first wrote down what i knew then began the Pythagorean Theorem. In using the squares, 10 was my Whole Number because it is the the closest perfect square before the number 117. I then got my Denominator by subtracting the two perfect squares from eachother. I got the numeratoe by subtracting the main number and the smaller perfect square. I couldn't end my answer with a Mixed fraction so I divided 17 to 21 to came up with a decimal form.

For the missing leg B I did the similar steps like the missing hypotenuse, but it changed when it came to the subtracting part. To get "B" you had to subtract A from C. After those steps you were back to the normal "missing side" steps.

For the missing leg A it was the same as Missing side B. The square is just in a different position during the subtracting steps.

Part 3:




Before I could do the Pythagorean Theorem, I first had to write down what I knew. The height of the frog from the tongue is 70 cm ( there is 100 cm in a m). The height of the door was 2m. And the distance from Lefrog and the door was 1.5 m. But I couldn't make a triangle just with that information. I had to find out what the height of the door is starting from the height of the tongue. So I had to subtract 70 from 200 which made 130cm or 1.3m. From there, I had my A (1.3) and my B (1.5). That's when I could use those numbers and the Pythagorean Theorem to solve the answer.


Part 4:

BubbleShare: Share photos - Powered by BubbleShare


Just in case you guys can't read the question. It says, " Mary had a dream to dunk. So one day she attempted. She stood at the free throw line, which was 20 feet away from the net. The basketball net's height is 10 feet tall. Mary is 4 feet tall for her feet to her arms. Her arms has a reach of 1 feet. How far and high does she have to jump to SLAM DUNK???

Answer:
First you had to write down what you knew. After that you had to make the triangle with the starting lengths. I subtracted 4 from 10 to get the starting height(A). I subtracted 1 from 20 to get the starting distance(B). Once I got those facts, I could finally do the Pythagorean Theorem. After I get the number for C², I could use the squares and get the Mixed Fraction. After that, I would just have to divide the Numerator to the Denominator, and add the answer to the Whole Number.

Marc's Third Growing Post

Part I:

A Pythagorean Triple is a right triangle that uses a set of whole numbers (1, 2, 3, etc..) used to satisfy the problem a² + b² = c².

This picture shows that

3² + 4² = 5² = 9 + 16 = 25.

Some other triples are:

6² + 8² = 10² = 36 + 64 = 100

You can use this same picture

to show 6² + 8² = 10² you just

have to change the 3 into a 6,

the 4 into a 8 and the 5 into a

10.

Part II:

BubbleShare: Share photos - Play some Online Games.

Part III:

You are locked you of your house, the only way in is an open window on the second floor 25 feet above the ground. Youre going to borrow a ladder from one of your neighbours. There are bushes around house so you have to put the ladder 10 feet away from the wall. What length of the ladder do you need to get to the window?

Part IV:

Mr. Jerema tells you that a right triangle has a hypotenuse of 13 and a leg of 5. She asks you to find the other leg of the triangle. What is your answer?

Karla's Pythagoras Growing Post

Part I:Pythagorean Triple

Mr. Jerema is teaching us about the Pythagorean Threom in which it states that if you add both legs of the right triangle(which is labelled a and b) is equal to the hypotenuse(which is labelled c) of the right triangle. (a squared + b squared= c squared.) This is how a Pythagorean theorem looks like:

To test if this theorem is right he taught us the Pythagorean Triple in which it uses a set of numbers (1,2,3,etc.). The numbers indicate the perfect squares which means there's no decimal used. For example: 3 squared + 4 squared= 5 squared

(9 + 16= 25)

a= 3 squared
b= 4 squared

c= 5 squared

3 squared= 9
4 squared= 16
5 squared= 25

But using another set of perfect square numbers we can test if this theorem really works. We could use the numbers 6 squared, 8 squared, and 10 squared.

(36 + 64=100)

a= 6 squared
b= 8 squared

c= 10 squared

6 squared= 36

8 squared= 64
10 squared= 100

Part II:Find the Missing Side

To find the missing side of any right triangle always remember the pythagorean formula (a squared + b squared=c squared). From this formula you can formulate other formulas you could use in finding the sides of a right triangle, like the legs or the hypotenuse.

A. HYPOTENUSE: for finding thre hypotenuse use the original formula. Always remember to find the hypotenuse it is where thew right angle always points.

example
BubbleShare: Share photos - Powered by BubbleShare

B. LEG(it's either a or b): write the original formula then formulate the formula you need for solving the problem. First thing is to write what you know to help you solve the problem.

example:BubbleShare: Share photos - Powered by BubbleShare

Part III: Word Problems

Example: You've just picked up a ground ball at first base, and you see the other team's player running towards the third base. How far do you have to throw the ball to get it from first base to third base, and throw the runner out?

Baseball Field

Answer: you should throw the ball 127.28 ft far.

Part IV: Make your own Word Problem

Example: If you're climbing up a mountain whose height is 36 m high and the base is 10 m long across. How long would the slope be if you have to roll a ball down to the other side of the mountain from the top of it?

Anne's Pythagoras Growing Post

Part 1: Describe what a Pythagorean Triple is and use your perfect square chart from 1 squared to 10 squared to find another one other than 3,4,5. (Note: You need a picture, not simply text.)

The definition that Mr. Jerema gave us was:
"A Pythagorean Triple is a right triangle that uses a set of whole numbers (1, 2, 3....etc) that satisfy A² + B² = C²"



A pythagorean Triple is a right triangle where the sides are in the ratio of a positive integer or whole number.
Examples are] 3:4:5, 6:8:10, 5:12:13, 9:12:15, 8:15:17 etc.
The formula is simple] a² + b² = c² OR x² + y² = z²
You can invert that formula with the examples like this] 3² x 4² = 5²


perfect square chart
1 x 1 = 1
2 x 2 = 4
3 x 3 = 9
4 x 4 = 16
5 x 5 = 25
6 x 6 = 36
7 x 7 = 49
8 x 8 = 64
9 x 9 = 81
10 x 10 = 100


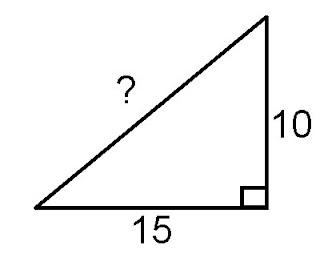
Part 2: Using embeddable web 2.0, describe how to find the missing side of a Right Triangle using the Pythagorean Theorem, show how to solve both for a missing leg and the hypotenuse (note: you may use numerical examples ie. a=4 b=6 c=?)



The first slides about the missing hypotenuse shows that the straight angle is 3 and the other straight angle is 4, is can be labelled either a or b. But let's say that a = 3 and b = 4. Now we have to find the missing side, since the right angle is in the bottom left corner, pretend to draw a little box to make sure that it is a right angle. Now if you can imagine the box, it would be pointing to the line.. which is the hypotenuse. We have to figure out what the hypotenuse is so we first:
write down what we already know
then write down the pythagorean thereom
then transfer that into the squared numbers
then transfer that into their standard form
then add it together and you get the number
but after you have to figure out the square unit for the number
in this case, the number is 25,
which is easy because the square unit is perfect since 5 squared = 25.

Part 3: Explain how to solve a Pythagoras word problem. Use one of the examples we covered in class (Worksheet A, B, LeFrog or Bonus Problem).

You've just picked up a ground ball at first base, and you see the other team's player runnig towards thrid base. How far do you have to throw the ball to get it from first base to thrid base, and runner out?



I highlighted half the square because it made a right triangle. Since all the sides are 90 squared except for the line running through third base and first base. That was the hypotenuse.

Part 4: Now that you have seen many Pythagorean problems, create your own word problem.

Two joggers run 8 miles north and then 5 miles west. What is the shortest distance, to the nearest tenth of a mile, they must travel to return to their starting point?