Hi, My scribe today is about that sheet that Mr . Harbeck told us to answer. The sheet I got was page 48 so if my questions are different than yours... too bad.
1. Enigma is __57___ old
Let x = age
- 1/3 x - 5 = 14
- x/3 - 5 = 14 + 5
- x = 19 x 3
- x= 57
- x/3 - 5 = 14
- 57/3 - 5 = 14
- 14 = 14
3. She rented ___26___ movies
Let x = movies
- 3x + 12 = 90
- 3x + 12 = 90 - 12
- x = 78/3
- x = 26
- 3x - 12 = 90
- 3(26) + 12 = 90
- 90 = 90
6. He ate ___22___ Chips
Let x = Chips
- 12x + 375 = 639
- 12x + 375 = 639 - 375
- x = 264/12
- x = 22
- 12x + 375 = 639
- 12(22) + 375 = 639
- 639 = 639
8. It took __13 _ Min.
Let x = minutes
- 25x + 75 = 400
- 25x + 75 = 400 - 75
- x = 375/26
- x = 13
- 25x + 75 = 400
- 25 (13) + 75 = 400
- 400 = 400
9. They need ___10800 wrapping paper
Let x = Wrapping paper
- 1/2 x - 400 = 5000
- x/2 - 400 = 5000 + 400
- x = 4600 x 2
- x = 10800
- x/2 - 400 = 5000
- 10800/2 - 400 = 5000
- 5000=5000
Just comment if i did something wrong. Thanks!
Wednesday, May 14, 2008
Tuesday, May 13, 2008
Kadille's Scribe Post
Geometric Problems
1. The length of the triangle is 3 times the width. the perimeter is 96 cm. Find the width and length. The sides are ____cm, _____cm. This is the diagram of the problem
 let x = w. align all sides and their labels. place the perimeter is equal to 96. add all the sides of the rectangle and place it beside the perimeter. then solve for x
let x = w. align all sides and their labels. place the perimeter is equal to 96. add all the sides of the rectangle and place it beside the perimeter. then solve for x
 this is the solution of x. x = 12. i substitute the sides' label beside it resulting 3x to be 3(12). then simplify it ( 3 (12) to 36) and place it above the given perimeter or total. add the simplified length of each side to check if the total will be the given perimeter.
this is the solution of x. x = 12. i substitute the sides' label beside it resulting 3x to be 3(12). then simplify it ( 3 (12) to 36) and place it above the given perimeter or total. add the simplified length of each side to check if the total will be the given perimeter.
and to finish this problem, we must finish it by answering the simple question.
The sides are 36 cm, 12 cm.
Note: this is very important. you will lose most of the marks if this is not done.
2. the length of a rectangle is 5m greater than the width. the perimeter is 150m. find the width and the length.
simple sentence: the sides are ____m, _____m.
diagram:

 align the sides with their labels beside them. include the perimeter under the line with its value 150 m far away beside it.
align the sides with their labels beside them. include the perimeter under the line with its value 150 m far away beside it.
 this is the solution of the problem.
this is the solution of the problem.
then answer the simple sentence: the sides are 40m , and 35 m.
3. the first side of a triangle is 8 m shorter than the second side. the third side is 45 times as long as the first side. the perimeter is 2 m. find the length of each side.
the simple sentence is : the sides are ___m, ___m, ____m.
diagram:
 this must be done to solve this problem
this must be done to solve this problem
 the solution of this problem
the solution of this problem
finish this problem by completing the simple sentence:
the sides are 3m, 11m, 12m.
4. the third side is 30 m shorter than twice the length of each congruent side. the perimeter is 570. find the length of each side
the sides are ___m, ____m, ____m.
diagram:


 the steps are indicated to the previous problems.
the steps are indicated to the previous problems.
finish this problem by completing the simple sentence:
the sides are 150m, 150m, 270m.
1. The length of the triangle is 3 times the width. the perimeter is 96 cm. Find the width and length. The sides are ____cm, _____cm. This is the diagram of the problem
This is to be done in solving this problem
and to finish this problem, we must finish it by answering the simple question.
The sides are 36 cm, 12 cm.
Note: this is very important. you will lose most of the marks if this is not done.
2. the length of a rectangle is 5m greater than the width. the perimeter is 150m. find the width and the length.
simple sentence: the sides are ____m, _____m.
diagram:
then answer the simple sentence: the sides are 40m , and 35 m.
3. the first side of a triangle is 8 m shorter than the second side. the third side is 45 times as long as the first side. the perimeter is 2 m. find the length of each side.
the simple sentence is : the sides are ___m, ___m, ____m.
diagram:
finish this problem by completing the simple sentence:
the sides are 3m, 11m, 12m.
4. the third side is 30 m shorter than twice the length of each congruent side. the perimeter is 570. find the length of each side
the sides are ___m, ____m, ____m.
diagram:
finish this problem by completing the simple sentence:
the sides are 150m, 150m, 270m.
 Today in class, Mr. Harbeck taught us how to do a problem solving question. Now, I'm going to scribe how to do/answer a problem solving question using numbers.
Today in class, Mr. Harbeck taught us how to do a problem solving question. Now, I'm going to scribe how to do/answer a problem solving question using numbers.
1. The second of two numbers is 4 times the first. Their sum is 50. Find the numbers.
The numbers are ____and____. (You can also write this at the end of the equation)
4x would be on the right side of the + sign, because it is the second number. The first number is x.
So, the equation would be like this:Let x = first #x + 4x = 50
5x = 50 (combined terms)
x = 10
The answer is 10, 40
You must write the formula x + 4x = 50
10 + 4(10) = 50
10 + 40 = 50
50 = 50
x = 10
4x = 40
2. The larger of two numbers is 12 more than the smaller. Their sum is 84. Find the numbers.
The numbers are ____,____,and ____. (You can also write this at the end of the equation)
Two other # would equal x because we don't know anything about them.
let x = small # 1 and small # 2
Two other # would equal x because we don't know anything about them.
let x = small # 1 and small # 2
x + 12 + x + x = 84
3x + 12 = 84 (combined terms)
-12 -123x = 72
x= 24
The answer is 36, 24, 24
3x + 12 = 84 (combined terms)
-12 -123x = 72
x= 24
The answer is 36, 24, 24
4. The second of two numbers is 5 more than twice the first. Their sum is 80. Find the numbers.
The numbers are ____,and ____. (You can also write this at the end of the equation)
let x = first#
The numbers are ____,and ____. (You can also write this at the end of the equation)
let x = first#
5 more than twice the first
2x + 5
the sum is 80
= 80
x + 2x + 5 = 80
3x + 5 = 80
- 5 -53
x = 75
3x = 25
2x+5 = 55
x = 25
The answer is 25, 55
6. Find two numbers whose sum is 92, if the first is 4 more than 7 times the second. Find the first number.
The numbers are ____,and ____. (You can also write this at the end of the equation)
let x = second #
(7x + 4) + x = 92
8x + 4 = 92 (combined terms)
- 4 -4
8x = 88
8x = 11
(7x + 4) + x = 92
8(11) + 4 = 92
88 + 4 = 92
92 = 92x
= 117
x + 4 = 81
The answer is 11, 92
8. Together, a necklace and a bracelet cost $192. Find the price of each if the necklace costs 3 times as much as the bracelet.
The price is____. (You can also write this at the end of the equation)
Let x = bracelet
3x = Necklace
3x + x = 19
24x = 192
4x = $48 ($48.00)
3x = 3
(48)= 144
x = 48
$144.00+$48.00
$192.00
The price of a bracelet is $48.00 and the necklace is $144.00.
Tuesday, May 6, 2008
Kevin Y's Scribe
My scribe is about Distributive Property
Terms that have the same variable parts are called like terms. The terms 2x, 4x, 5x are like terms. Unlike terms are 6x, 3x(squared), 4y. Only like terms can be combined.
To expand an expression with brackets means to remove the brackets by multiplying. This is done using the distributive property.
Distributive Property has 3 ways to do it.
For example for 3(y + 6)
Way #1
3(y + 6) = 3y + 4 x 6
= 3y + 18
Way #2
Way #3
x + 6
x + 6
x + 6
3x + 18
So Distrubtive Property is basicaly expanding the expression.
The best way to use distrubtive property will probably be Way #3 and #1 if Way #2 helps you understand better then use it.
Monday, May 5, 2008
Melissa's Scribe Post Equation Solving : Addition
The steps for Equation Solving for addition

n+4=9
1.)
Isolate the variable
n+4= 9
2.)
Cancel the constant (integer) using its opposite to make
zero pairs.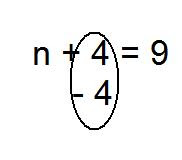 3.) BALANCE
3.) BALANCE
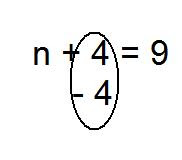 3.) BALANCE
3.) BALANCE
4.) SUBSTITUTE TO CHECK

Ivanne's Scribe Post: Equation Solving (Multiplying & Dividing)
Mariya's Scribe Post
When Mr. Jerema came in and substitute for Mr. Harbeck, we did some work on algebra.
We had to do two questions on a piece of blue sheet that Mr. Jerema gave us and we had to draw a table, describe the recursive pattern, describe the functional pattern and do the algebraic equation. After doing all of that, we had to draw a graph on graph paper.
So, the first one we had to do was called Car Repairs. On Car Repairs, Mr. Jerema drew a graph on the board, that looked like this.

After that, we do the algebraic equation and we described it in words.

Our second one was called Harbeck's Training, and we had to do the same thing as Car Repairs, but with different numbers.
Graph of Harbeck's Training

Table and recursive pattern:

Algebraic equation and describing it in words.

Janns Scribe Post
Sorry this scribe was waaay late
This scribe is about the algebra test 2.0 and ill tell you all about it and what the answers are!
This is part 1 of the test ill give you 3 possible answers for each one.
1) 2x-9 - 2 times a number decreased by 9
- twice a number decreased 9
- 2 groups of a numbers decreased by 9
2) 10-4x - 10 decreased by 4 times a number
- 10 decreased by 4 groups of a number
- 10 deminished by 4 sets of a number
3) 5(x-8) - 5 groups of the difference of a number and 8
- a number decreased by 8 times 5
- 5 times a number decreased by 8
4) 7(x+5) - 7 sets of the sum of a number and 5
- the sum of a number and 5 times 7
- a number combined with 5 times 7
This is part 2 of the test , there is only one answer possible for each
5) 6 centimeters more than two thirds of length X = 6 + 2/3 X
6) three times the sum of a number and 2 = 3(n+2)
7) nine decreased by 2 times a number = 9 - 2n
8) four less than five times a number = 5n - 4
This is the chart questions on the other page.
The following Graph shows the first 4 terms of a pattern

A) Create a Chart that shows the first 10 terms of the pattern
 B) Write the algebraic Express for the relation ship between hours spent walking and the number of kilometres walked
B) Write the algebraic Express for the relation ship between hours spent walking and the number of kilometres walked
This scribe is about the algebra test 2.0 and ill tell you all about it and what the answers are!
This is part 1 of the test ill give you 3 possible answers for each one.
1) 2x-9 - 2 times a number decreased by 9
- twice a number decreased 9
- 2 groups of a numbers decreased by 9
2) 10-4x - 10 decreased by 4 times a number
- 10 decreased by 4 groups of a number
- 10 deminished by 4 sets of a number
3) 5(x-8) - 5 groups of the difference of a number and 8
- a number decreased by 8 times 5
- 5 times a number decreased by 8
4) 7(x+5) - 7 sets of the sum of a number and 5
- the sum of a number and 5 times 7
- a number combined with 5 times 7
This is part 2 of the test , there is only one answer possible for each
5) 6 centimeters more than two thirds of length X = 6 + 2/3 X
6) three times the sum of a number and 2 = 3(n+2)
7) nine decreased by 2 times a number = 9 - 2n
8) four less than five times a number = 5n - 4
This is the chart questions on the other page.
The following Graph shows the first 4 terms of a pattern

A) Create a Chart that shows the first 10 terms of the pattern
- Hours x 4 -1 = Km walks
- 4x -1 = y
X = hours
Y= Km walked
C) Using your algebraic expression determine how far they could walk after 50 hours
50 = 4x - 1
= 4(200) - 1
= 199 Km
This test was out of 16. Thanks!
Friday, May 2, 2008
Marc's Scribe
I <3>

Y Axis = Triangles:2 3 4 5 6 7
X Axis = Figure #: 1 2 3 4 5 6
Y = starts with 2 triangles and add one triangle per figure
X = Starts with figure one and adds 1 figure everytime
Recursive pattern
You add 1 to the figure # to make Y
Let X = Figure #
X + 1
I Got Steak In My Teeth:
X Axis = Figure #: 1 2 3 4 5 6
Y = Start with 3 toothpicks and add 2 toothpicks everytime
X = Start with figure one and add 1 figure number everytime
For each figure, you add two toothpicks from the last figure. Multiply the figure by two and add one
2x + 1 = Y
Thursday, May 1, 2008
Angelo's Scribe of Test Number One
On part one of the math test, we were given eight algebraic equations. Half were written out in numeric form, the other half, as written in words. For the numeric equations, we had to write down the correct word form for that equation. For example, the numerical equation would be 7x + 5x, and then we'd have to write it as seven times a number increased by 5 times a number. Like this:

When we were dealing with the written form, the equation would be like, nine centimeters less than 3/4 of length x. Then we'd have to write it into a numeric equation, which would be 3/4x - 9. Like this:

These type of questions ended the first part.
For Part Two, we were to complete a graph. We were given a graph and the first 3 figures of a pattern. The first 3 figures of the pattern were these:

The graph looked like this :
 You had to fill three sides of the graph with the appropriate title.
You had to fill three sides of the graph with the appropriate title.
We also had to create a T - Table showing our understanding of the pattern. It kind of looked like this :

After we completed the chart, and had it all filled out, we had to come up with an algebraic equation on how you would get from x to y. This was the equation needed:

You need to have the x equal the figure number and the y equal the number of squares. In our test these were what we needed to get the questions correct:

This ends the test, hope you guys learned a lot!!!

When we were dealing with the written form, the equation would be like, nine centimeters less than 3/4 of length x. Then we'd have to write it into a numeric equation, which would be 3/4x - 9. Like this:

These type of questions ended the first part.
For Part Two, we were to complete a graph. We were given a graph and the first 3 figures of a pattern. The first 3 figures of the pattern were these:

The graph looked like this :
 You had to fill three sides of the graph with the appropriate title.
You had to fill three sides of the graph with the appropriate title.We also had to create a T - Table showing our understanding of the pattern. It kind of looked like this :

After we completed the chart, and had it all filled out, we had to come up with an algebraic equation on how you would get from x to y. This was the equation needed:

You need to have the x equal the figure number and the y equal the number of squares. In our test these were what we needed to get the questions correct:

This ends the test, hope you guys learned a lot!!!
Alex's Scribe Post
Algetiles
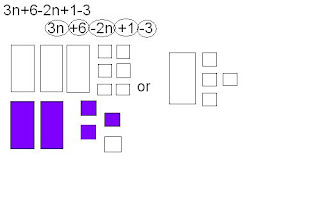
Think! What did I do to get rid of the coloured squares?
Today in class, Mr. Harbeck gave us small pieces of tiles. We call it Algetiles. We learned something new about algebra using algetiles, and it's something like this:
Terms
n = variable
n = variable
+ and - = integer (constant)

By using algetiles, we can find out how an algebraic expression looks like.
Example:

Think! What did I do to get rid of the coloured squares?
Subscribe to:
Comments (Atom)