Janns Scribe

Hi, My scribe today is about that sheet that Mr . Harbeck told us to answer. The sheet I got was page 48 so if my questions are different than yours... too bad.

1. Enigma is __57___ old
Let x = age
- 1/3 x - 5 = 14
- x/3 - 5 = 14 + 5
- x = 19 x 3
- x= 57
- x/3 - 5 = 14
- 57/3 - 5 = 14
- 14 = 14

3. She rented ___26___ movies
Let x = movies
- 3x + 12 = 90
- 3x + 12 = 90 - 12
- x = 78/3
- x = 26
- 3x - 12 = 90
- 3(26) + 12 = 90
- 90 = 90

6. He ate ___22___ Chips
Let x = Chips
- 12x + 375 = 639
- 12x + 375 = 639 - 375
- x = 264/12
- x = 22
- 12x + 375 = 639
- 12(22) + 375 = 639
- 639 = 639

8. It took __13 _ Min.
Let x = minutes
- 25x + 75 = 400
- 25x + 75 = 400 - 75
- x = 375/26
- x = 13
- 25x + 75 = 400
- 25 (13) + 75 = 400
- 400 = 400

9. They need ___10800 wrapping paper
Let x = Wrapping paper
- 1/2 x - 400 = 5000
- x/2 - 400 = 5000 + 400
- x = 4600 x 2
- x = 10800
- x/2 - 400 = 5000
- 10800/2 - 400 = 5000
- 5000=5000

Just comment if i did something wrong. Thanks!

Kadille's Scribe Post

Geometric Problems

1. The length of the triangle is 3 times the width. the perimeter is 96 cm. Find the width and length. The sides are ____cm, _____cm. This is the diagram of the problem

This is to be done in solving this problem

let x = w. align all sides and their labels. place the perimeter is equal to 96. add all the sides of the rectangle and place it beside the perimeter. then solve for x










this is the solution of x. x = 12. i substitute the sides' label beside it resulting 3x to be 3(12). then simplify it ( 3 (12) to 36) and place it above the given perimeter or total. add the simplified length of each side to check if the total will be the given perimeter.
and to finish this problem, we must finish it by answering the simple question.

The sides are 36 cm, 12 cm.
Note: this is very important. you will lose most of the marks if this is not done.


2. the length of a rectangle is 5m greater than the width. the perimeter is 150m. find the width and the length.

simple sentence: the sides are ____m, _____m.

diagram:

align the sides with their labels beside them. include the perimeter under the line with its value 150 m far away beside it.

this is the solution of the problem.

then answer the simple sentence: the sides are 40m , and 35 m.










3. the first side of a triangle is 8 m shorter than the second side. the third side is 45 times as long as the first side. the perimeter is 2 m. find the length of each side.



the simple sentence is : the sides are ___m, ___m, ____m.


diagram:













this must be done to solve this problem











the solution of this problem



finish this problem by completing the simple sentence:

the sides are 3m, 11m, 12m.





4. the third side is 30 m shorter than twice the length of each congruent side. the perimeter is 570. find the length of each side

the sides are ___m, ____m, ____m.


diagram:














the steps are indicated to the previous problems.


finish this problem by completing the simple sentence:

the sides are 150m, 150m, 270m.

NADINE'S SCRIBE POST (PROBLEM SOLVING USING NUMBERS)

Today in class, Mr. Harbeck taught us how to do a problem solving question. Now, I'm going to scribe how to do/answer a problem solving question using numbers.

1. The second of two numbers is 4 times the first. Their sum is 50. Find the numbers.

The numbers are ____and____. (You can also write this at the end of the equation)

4x would be on the right side of the + sign, because it is the second number. The first number is x.

So, the equation would be like this:Let x = first #x + 4x = 50

5x = 50 (combined terms)

x = 10

The answer is 10, 40

You must write the formula x + 4x = 50

10 + 4(10) = 50

10 + 40 = 50

50 = 50

x = 10

4x = 40

2. The larger of two numbers is 12 more than the smaller. Their sum is 84. Find the numbers.

The numbers are ____,____,and ____. (You can also write this at the end of the equation)
Two other # would equal x because we don't know anything about them.
let x = small # 1 and small # 2

x + 12 + x + x = 84
3x + 12 = 84 (combined terms)
-12 -123x = 72
x= 24
The answer is 36, 24, 24

4. The second of two numbers is 5 more than twice the first. Their sum is 80. Find the numbers.
The numbers are ____,and ____. (You can also write this at the end of the equation)
let x = first#

5 more than twice the first

2x + 5

the sum is 80

= 80

x + 2x + 5 = 80

3x + 5 = 80

- 5 -53

x = 75

3x = 25

2x+5 = 55

x = 25

The answer is 25, 55

6. Find two numbers whose sum is 92, if the first is 4 more than 7 times the second. Find the first number.

The numbers are ____,and ____. (You can also write this at the end of the equation)

let x = second #

(7x + 4) + x = 92

8x + 4 = 92 (combined terms)

- 4 -4

8x = 88

8x = 11

(7x + 4) + x = 92

8(11) + 4 = 92

88 + 4 = 92

92 = 92x

= 117

x + 4 = 81

The answer is 11, 92

8. Together, a necklace and a bracelet cost $192. Find the price of each if the necklace costs 3 times as much as the bracelet.

The price is____. (You can also write this at the end of the equation)

Let x = bracelet

3x = Necklace

3x + x = 19

24x = 192

4x = $48 ($48.00)

3x = 3

(48)= 144

x = 48

$144.00+$48.00

$192.00

The price of a bracelet is $48.00 and the necklace is $144.00.

Kevin Y's Scribe

My scribe is about Distributive Property

Terms that have the same variable parts are called like terms. The terms 2x, 4x, 5x are like terms. Unlike terms are 6x, 3x(squared), 4y. Only like terms can be combined.

To expand an expression with brackets means to remove the brackets by multiplying. This is done using the distributive property.

Distributive Property has 3 ways to do it.

For example for 3(y + 6)

Way #1

3(y + 6) = 3y + 4 x 6

= 3y + 18

Way #2

Way #3
x + 6
x + 6
x + 6
3x + 18

So Distrubtive Property is basicaly expanding the expression.
The best way to use distrubtive property will probably be Way #3 and #1 if Way #2 helps you understand better then use it.

Melissa's Scribe Post Equation Solving : Addition

The steps for Equation Solving for addition

n+4=9

1.)

Isolate the variable

n+4= 9

2.)

Cancel the constant (integer) using its opposite to make

zero pairs.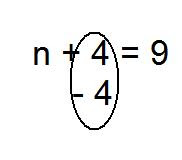3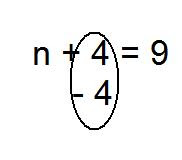.) BALANCE

4.) SUBSTITUTE TO CHECK

Ivanne's Scribe Post: Equation Solving (Multiplying & Dividing)

The steps for doing this equation solving for multiplying and dividing are:

3n = 12

1.) Isolate using the variables

3n = 12

2.) Cancel using the opposite operation to make only 1 variable
















3.) Balance the equation by substituting the value of n.













*i just put the steps 3 and 4 together...

Mariya's Scribe Post

When Mr. Jerema came in and substitute for Mr. Harbeck, we did some work on algebra.

We had to do two questions on a piece of blue sheet that Mr. Jerema gave us and we had to draw a table, describe the recursive pattern, describe the functional pattern and do the algebraic equation. After doing all of that, we had to draw a graph on graph paper.

So, the first one we had to do was called Car Repairs. On Car Repairs, Mr. Jerema drew a graph on the board, that looked like this.

We then had to draw a table and describe the recursive pattern.

After that, we do the algebraic equation and we described it in words.

Our second one was called Harbeck's Training, and we had to do the same thing as Car Repairs, but with different numbers.

Graph of Harbeck's Training

Table and recursive pattern:

Algebraic equation and describing it in words.